Mandelbrot at higher powersWritten by Paul BourkeFebruary 2004
The traditional Mandelbrot is created by considering the behaviour of the series zn+1 = zn2 + zo for each position zo on the complex plane. A more general equation might be zn+1 = znM + zo. The resulting shapes are less frequently explored, a graphical exploration of M space is given below. Integer powers M = 1 zn+1 = zn1 + zo This is of course hardly very interesting, nor fractal. M = 2  zn+1 = zn2 + zo The traditional Mandelbrot, M = 2. M = 3  zn+1 = zn3 + zo M = 4  zn+1 = zn4 + zo M = 5  zn+1 = zn5 + zo M = 6  zn+1 = zn6 + zo M = 7  zn+1 = zn7 + zo M = 8  zn+1 = zn8 + zo M = 10  zn+1 = zn10 + zo
 Non-Integer powers
M = 2.1 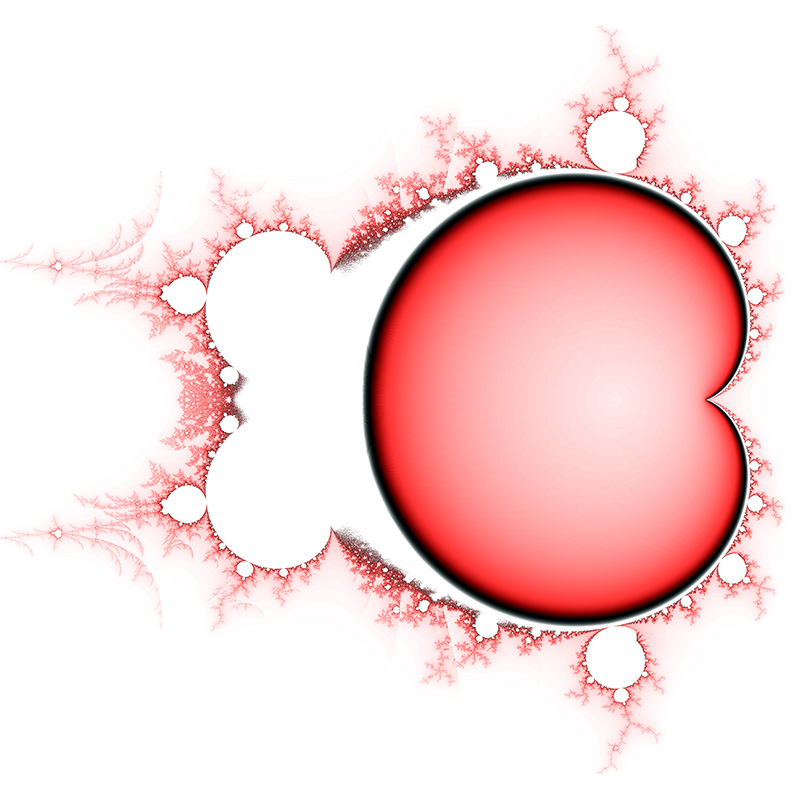 zn+1 = zn2.1 + zo

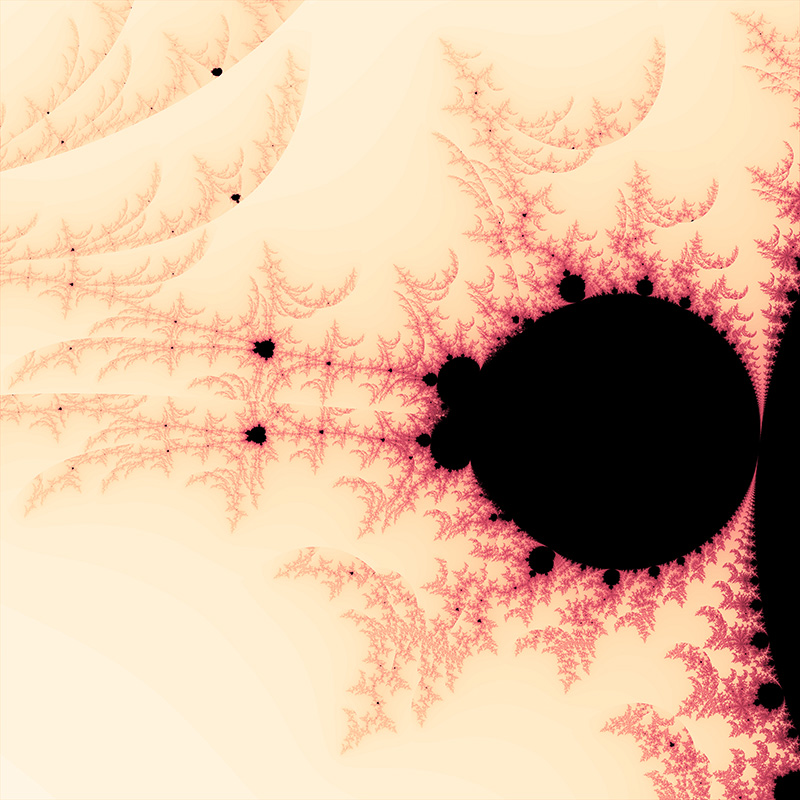 M = 2.3  zn+1 = zn2.3 + zo M = 2.5  zn+1 = zn2.5 + zo M = 2.7  zn+1 = zn2.7 + zo Negative powers
M = -1  zn+1 = zn-1 + zo M = -2  zn+1 = zn-2 + zo M = -3  zn+1 = zn-3 + zo M = -10  zn+1 = zn-10 + zo
 M = -2.3  zn+1 = zn-2.3 + zo M = -2.5  zn+1 = zn-2.5 + zo |