Polygonising a scalar fieldAlso known as: "3D Contouring", "Marching Cubes", "Surface Reconstruction"
Written by Paul Bourke
Based on tables by Cory Gene Bloyd along with additional example source code
marchingsource.cpp
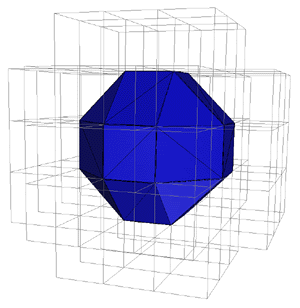
This document describes an algorithm for creating a polygonal surface representation of an isosurface of a 3D scalar field. A common name for this type of problem is the so called "marching cubes" algorithm. It combines simplicity with high speed since it works almost entirely on lookup tables. There are many applications for this type of technique, two very common ones are:
The fundamental problem is to form a facet approximation to an isosurface through a scalar field sampled on a rectangular 3D grid. Given one grid cell defined by its vertices and scalar values at each vertex, it is necessary to create planar facets that best represent the isosurface through that grid cell. The isosurface may not be pass through the grid cell, it may cut off any one of the vertices, or it may pass through in any one of a number of more complicated ways. Each possibility will be characterised by the number of vertices that have values above or below the isosurface. If one vertex is above the isosurface say and an adjacent vertex is below the isosurface then we know the isosurface cuts the edge between these two vertices. The position that it cuts the edge will be linearly interpolated, the ratio of the length between the two vertices will be the same as the ratio of the isosurface value to the values at the vertices of the grid cell. The indexing convention for vertices and edges used in the algorithm are shown below 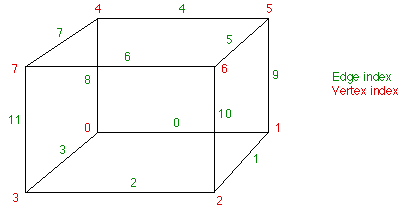
If for example the value at vertex 3 is below the isosurface value and all the values at all the other vertices were above the isosurface value then we would create a triangular facet which cuts through edges 2,3, and 11. The exact position of the vertices of the triangular facet depend on the relationship of the isosurface value to the values at the vertices 3-2, 3-0, 3-7 respectively. 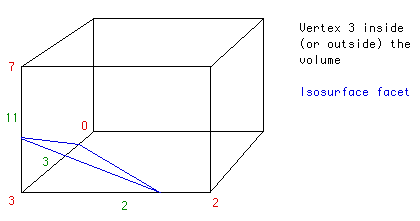
What makes the algorithm "difficult" are the large number (256) of possible combinations and the need to derive a consistent facet combination for each solution so that facets from adjacent grid cells connect together correctly. The first part of the algorithm uses a table (edgeTable) which maps the vertices under the isosurface to the intersecting edges. An 8 bit index is formed where each bit corresponds to a vertex. cubeindex = 0; if (grid.val[0] < isolevel) cubeindex |= 1; if (grid.val[1] < isolevel) cubeindex |= 2; if (grid.val[2] < isolevel) cubeindex |= 4; if (grid.val[3] < isolevel) cubeindex |= 8; if (grid.val[4] < isolevel) cubeindex |= 16; if (grid.val[5] < isolevel) cubeindex |= 32; if (grid.val[6] < isolevel) cubeindex |= 64; if (grid.val[7] < isolevel) cubeindex |= 128; Looking up the edge table returns a 12 bit number, each bit corresponding to an edge, 0 if the edge isn't cut by the isosurface, 1 if the edge is cut by the isosurface. If none of the edges are cut the table returns a 0, this occurs when cubeindex is 0 (all vertices below the isosurface) or 0xff (all vertices above the isosurface). Using the example earlier where only vertex 3 was below the isosurface, cubeindex would equal 0000 1000 or 8. edgeTable[8] = 1000 0000 1100. This means that edge 2,3, and 11 are intersected by the isosurface. The intersection points are now calculated by linear interpolation. If P1 and P2 are the vertices of a cut edge and V1 and V2 are the scalar values at each vertex, the the intersection point P is given by
The last part of the algorithm involves forming the correct facets from the positions that the isosurface intersects the edges of the grid cell. Again a table (triTable) is used which this time uses the same cubeindex but allows the vertex sequence to be looked up for as many triangular facets are necessary to represent the isosurface within the grid cell. There at most 5 triangular facets necessary.
Back to our example, in the previous step we calculate the intersecting
points along edge 2,3, and 11. The 8th element in triTable is
Lets say vertex 0 and 3 are below the isosurface. cubeindex will
then be 0000 1001 == 9.
The 9th entry into the egdeTable is
905hex == 1001 0000 0101
which means edge 11,8,2, and 0 are cut and so we work out the vertices of the
intersection of the isosurface with those edges.
One very desirable control when polygonising a field where the values are known or can be interpolated anywhere in space is the resolution of the sampling grid. This allows course or fine approximation to the isosurface to be generated depending on the smoothness required and/or the processing power available to display the surface. The following example is of two "bobby molecules" as specified by Blinn, generated at different grid sizes. 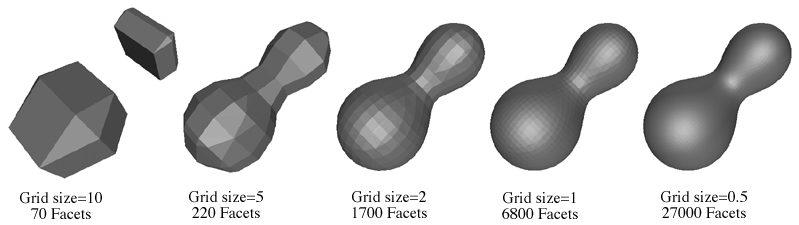
Source code
typedef struct {
XYZ p[3];
} TRIANGLE;
typedef struct {
XYZ p[8];
double val[8];
} GRIDCELL;
/*
Given a grid cell and an isolevel, calculate the triangular
facets required to represent the isosurface through the cell.
Return the number of triangular facets, the array "triangles"
will be loaded up with the vertices at most 5 triangular facets.
0 will be returned if the grid cell is either totally above
of totally below the isolevel.
*/
int Polygonise(GRIDCELL grid,double isolevel,TRIANGLE *triangles)
{
int i,ntriang;
int cubeindex;
XYZ vertlist[12];
int edgeTable[256]={
0x0 , 0x109, 0x203, 0x30a, 0x406, 0x50f, 0x605, 0x70c,
0x80c, 0x905, 0xa0f, 0xb06, 0xc0a, 0xd03, 0xe09, 0xf00,
0x190, 0x99 , 0x393, 0x29a, 0x596, 0x49f, 0x795, 0x69c,
0x99c, 0x895, 0xb9f, 0xa96, 0xd9a, 0xc93, 0xf99, 0xe90,
0x230, 0x339, 0x33 , 0x13a, 0x636, 0x73f, 0x435, 0x53c,
0xa3c, 0xb35, 0x83f, 0x936, 0xe3a, 0xf33, 0xc39, 0xd30,
0x3a0, 0x2a9, 0x1a3, 0xaa , 0x7a6, 0x6af, 0x5a5, 0x4ac,
0xbac, 0xaa5, 0x9af, 0x8a6, 0xfaa, 0xea3, 0xda9, 0xca0,
0x460, 0x569, 0x663, 0x76a, 0x66 , 0x16f, 0x265, 0x36c,
0xc6c, 0xd65, 0xe6f, 0xf66, 0x86a, 0x963, 0xa69, 0xb60,
0x5f0, 0x4f9, 0x7f3, 0x6fa, 0x1f6, 0xff , 0x3f5, 0x2fc,
0xdfc, 0xcf5, 0xfff, 0xef6, 0x9fa, 0x8f3, 0xbf9, 0xaf0,
0x650, 0x759, 0x453, 0x55a, 0x256, 0x35f, 0x55 , 0x15c,
0xe5c, 0xf55, 0xc5f, 0xd56, 0xa5a, 0xb53, 0x859, 0x950,
0x7c0, 0x6c9, 0x5c3, 0x4ca, 0x3c6, 0x2cf, 0x1c5, 0xcc ,
0xfcc, 0xec5, 0xdcf, 0xcc6, 0xbca, 0xac3, 0x9c9, 0x8c0,
0x8c0, 0x9c9, 0xac3, 0xbca, 0xcc6, 0xdcf, 0xec5, 0xfcc,
0xcc , 0x1c5, 0x2cf, 0x3c6, 0x4ca, 0x5c3, 0x6c9, 0x7c0,
0x950, 0x859, 0xb53, 0xa5a, 0xd56, 0xc5f, 0xf55, 0xe5c,
0x15c, 0x55 , 0x35f, 0x256, 0x55a, 0x453, 0x759, 0x650,
0xaf0, 0xbf9, 0x8f3, 0x9fa, 0xef6, 0xfff, 0xcf5, 0xdfc,
0x2fc, 0x3f5, 0xff , 0x1f6, 0x6fa, 0x7f3, 0x4f9, 0x5f0,
0xb60, 0xa69, 0x963, 0x86a, 0xf66, 0xe6f, 0xd65, 0xc6c,
0x36c, 0x265, 0x16f, 0x66 , 0x76a, 0x663, 0x569, 0x460,
0xca0, 0xda9, 0xea3, 0xfaa, 0x8a6, 0x9af, 0xaa5, 0xbac,
0x4ac, 0x5a5, 0x6af, 0x7a6, 0xaa , 0x1a3, 0x2a9, 0x3a0,
0xd30, 0xc39, 0xf33, 0xe3a, 0x936, 0x83f, 0xb35, 0xa3c,
0x53c, 0x435, 0x73f, 0x636, 0x13a, 0x33 , 0x339, 0x230,
0xe90, 0xf99, 0xc93, 0xd9a, 0xa96, 0xb9f, 0x895, 0x99c,
0x69c, 0x795, 0x49f, 0x596, 0x29a, 0x393, 0x99 , 0x190,
0xf00, 0xe09, 0xd03, 0xc0a, 0xb06, 0xa0f, 0x905, 0x80c,
0x70c, 0x605, 0x50f, 0x406, 0x30a, 0x203, 0x109, 0x0 };
int triTable[256][16] =
{{-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 8, 3, 9, 8, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 1, 2, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 2, 10, 0, 2, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 8, 3, 2, 10, 8, 10, 9, 8, -1, -1, -1, -1, -1, -1, -1},
{3, 11, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 11, 2, 8, 11, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 9, 0, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 11, 2, 1, 9, 11, 9, 8, 11, -1, -1, -1, -1, -1, -1, -1},
{3, 10, 1, 11, 10, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 10, 1, 0, 8, 10, 8, 11, 10, -1, -1, -1, -1, -1, -1, -1},
{3, 9, 0, 3, 11, 9, 11, 10, 9, -1, -1, -1, -1, -1, -1, -1},
{9, 8, 10, 10, 8, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 7, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 3, 0, 7, 3, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 1, 9, 4, 7, 1, 7, 3, 1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 4, 7, 3, 0, 4, 1, 2, 10, -1, -1, -1, -1, -1, -1, -1},
{9, 2, 10, 9, 0, 2, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1},
{2, 10, 9, 2, 9, 7, 2, 7, 3, 7, 9, 4, -1, -1, -1, -1},
{8, 4, 7, 3, 11, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 4, 7, 11, 2, 4, 2, 0, 4, -1, -1, -1, -1, -1, -1, -1},
{9, 0, 1, 8, 4, 7, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1},
{4, 7, 11, 9, 4, 11, 9, 11, 2, 9, 2, 1, -1, -1, -1, -1},
{3, 10, 1, 3, 11, 10, 7, 8, 4, -1, -1, -1, -1, -1, -1, -1},
{1, 11, 10, 1, 4, 11, 1, 0, 4, 7, 11, 4, -1, -1, -1, -1},
{4, 7, 8, 9, 0, 11, 9, 11, 10, 11, 0, 3, -1, -1, -1, -1},
{4, 7, 11, 4, 11, 9, 9, 11, 10, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 4, 0, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 5, 4, 1, 5, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 5, 4, 8, 3, 5, 3, 1, 5, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 9, 5, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 8, 1, 2, 10, 4, 9, 5, -1, -1, -1, -1, -1, -1, -1},
{5, 2, 10, 5, 4, 2, 4, 0, 2, -1, -1, -1, -1, -1, -1, -1},
{2, 10, 5, 3, 2, 5, 3, 5, 4, 3, 4, 8, -1, -1, -1, -1},
{9, 5, 4, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 11, 2, 0, 8, 11, 4, 9, 5, -1, -1, -1, -1, -1, -1, -1},
{0, 5, 4, 0, 1, 5, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1},
{2, 1, 5, 2, 5, 8, 2, 8, 11, 4, 8, 5, -1, -1, -1, -1},
{10, 3, 11, 10, 1, 3, 9, 5, 4, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 5, 0, 8, 1, 8, 10, 1, 8, 11, 10, -1, -1, -1, -1},
{5, 4, 0, 5, 0, 11, 5, 11, 10, 11, 0, 3, -1, -1, -1, -1},
{5, 4, 8, 5, 8, 10, 10, 8, 11, -1, -1, -1, -1, -1, -1, -1},
{9, 7, 8, 5, 7, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 3, 0, 9, 5, 3, 5, 7, 3, -1, -1, -1, -1, -1, -1, -1},
{0, 7, 8, 0, 1, 7, 1, 5, 7, -1, -1, -1, -1, -1, -1, -1},
{1, 5, 3, 3, 5, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 7, 8, 9, 5, 7, 10, 1, 2, -1, -1, -1, -1, -1, -1, -1},
{10, 1, 2, 9, 5, 0, 5, 3, 0, 5, 7, 3, -1, -1, -1, -1},
{8, 0, 2, 8, 2, 5, 8, 5, 7, 10, 5, 2, -1, -1, -1, -1},
{2, 10, 5, 2, 5, 3, 3, 5, 7, -1, -1, -1, -1, -1, -1, -1},
{7, 9, 5, 7, 8, 9, 3, 11, 2, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 7, 9, 7, 2, 9, 2, 0, 2, 7, 11, -1, -1, -1, -1},
{2, 3, 11, 0, 1, 8, 1, 7, 8, 1, 5, 7, -1, -1, -1, -1},
{11, 2, 1, 11, 1, 7, 7, 1, 5, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 8, 8, 5, 7, 10, 1, 3, 10, 3, 11, -1, -1, -1, -1},
{5, 7, 0, 5, 0, 9, 7, 11, 0, 1, 0, 10, 11, 10, 0, -1},
{11, 10, 0, 11, 0, 3, 10, 5, 0, 8, 0, 7, 5, 7, 0, -1},
{11, 10, 5, 7, 11, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{10, 6, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 0, 1, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 8, 3, 1, 9, 8, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1},
{1, 6, 5, 2, 6, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 6, 5, 1, 2, 6, 3, 0, 8, -1, -1, -1, -1, -1, -1, -1},
{9, 6, 5, 9, 0, 6, 0, 2, 6, -1, -1, -1, -1, -1, -1, -1},
{5, 9, 8, 5, 8, 2, 5, 2, 6, 3, 2, 8, -1, -1, -1, -1},
{2, 3, 11, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 0, 8, 11, 2, 0, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, 2, 3, 11, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1},
{5, 10, 6, 1, 9, 2, 9, 11, 2, 9, 8, 11, -1, -1, -1, -1},
{6, 3, 11, 6, 5, 3, 5, 1, 3, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 11, 0, 11, 5, 0, 5, 1, 5, 11, 6, -1, -1, -1, -1},
{3, 11, 6, 0, 3, 6, 0, 6, 5, 0, 5, 9, -1, -1, -1, -1},
{6, 5, 9, 6, 9, 11, 11, 9, 8, -1, -1, -1, -1, -1, -1, -1},
{5, 10, 6, 4, 7, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 3, 0, 4, 7, 3, 6, 5, 10, -1, -1, -1, -1, -1, -1, -1},
{1, 9, 0, 5, 10, 6, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1},
{10, 6, 5, 1, 9, 7, 1, 7, 3, 7, 9, 4, -1, -1, -1, -1},
{6, 1, 2, 6, 5, 1, 4, 7, 8, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 5, 5, 2, 6, 3, 0, 4, 3, 4, 7, -1, -1, -1, -1},
{8, 4, 7, 9, 0, 5, 0, 6, 5, 0, 2, 6, -1, -1, -1, -1},
{7, 3, 9, 7, 9, 4, 3, 2, 9, 5, 9, 6, 2, 6, 9, -1},
{3, 11, 2, 7, 8, 4, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1},
{5, 10, 6, 4, 7, 2, 4, 2, 0, 2, 7, 11, -1, -1, -1, -1},
{0, 1, 9, 4, 7, 8, 2, 3, 11, 5, 10, 6, -1, -1, -1, -1},
{9, 2, 1, 9, 11, 2, 9, 4, 11, 7, 11, 4, 5, 10, 6, -1},
{8, 4, 7, 3, 11, 5, 3, 5, 1, 5, 11, 6, -1, -1, -1, -1},
{5, 1, 11, 5, 11, 6, 1, 0, 11, 7, 11, 4, 0, 4, 11, -1},
{0, 5, 9, 0, 6, 5, 0, 3, 6, 11, 6, 3, 8, 4, 7, -1},
{6, 5, 9, 6, 9, 11, 4, 7, 9, 7, 11, 9, -1, -1, -1, -1},
{10, 4, 9, 6, 4, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 10, 6, 4, 9, 10, 0, 8, 3, -1, -1, -1, -1, -1, -1, -1},
{10, 0, 1, 10, 6, 0, 6, 4, 0, -1, -1, -1, -1, -1, -1, -1},
{8, 3, 1, 8, 1, 6, 8, 6, 4, 6, 1, 10, -1, -1, -1, -1},
{1, 4, 9, 1, 2, 4, 2, 6, 4, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 8, 1, 2, 9, 2, 4, 9, 2, 6, 4, -1, -1, -1, -1},
{0, 2, 4, 4, 2, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 3, 2, 8, 2, 4, 4, 2, 6, -1, -1, -1, -1, -1, -1, -1},
{10, 4, 9, 10, 6, 4, 11, 2, 3, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 2, 2, 8, 11, 4, 9, 10, 4, 10, 6, -1, -1, -1, -1},
{3, 11, 2, 0, 1, 6, 0, 6, 4, 6, 1, 10, -1, -1, -1, -1},
{6, 4, 1, 6, 1, 10, 4, 8, 1, 2, 1, 11, 8, 11, 1, -1},
{9, 6, 4, 9, 3, 6, 9, 1, 3, 11, 6, 3, -1, -1, -1, -1},
{8, 11, 1, 8, 1, 0, 11, 6, 1, 9, 1, 4, 6, 4, 1, -1},
{3, 11, 6, 3, 6, 0, 0, 6, 4, -1, -1, -1, -1, -1, -1, -1},
{6, 4, 8, 11, 6, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 10, 6, 7, 8, 10, 8, 9, 10, -1, -1, -1, -1, -1, -1, -1},
{0, 7, 3, 0, 10, 7, 0, 9, 10, 6, 7, 10, -1, -1, -1, -1},
{10, 6, 7, 1, 10, 7, 1, 7, 8, 1, 8, 0, -1, -1, -1, -1},
{10, 6, 7, 10, 7, 1, 1, 7, 3, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 6, 1, 6, 8, 1, 8, 9, 8, 6, 7, -1, -1, -1, -1},
{2, 6, 9, 2, 9, 1, 6, 7, 9, 0, 9, 3, 7, 3, 9, -1},
{7, 8, 0, 7, 0, 6, 6, 0, 2, -1, -1, -1, -1, -1, -1, -1},
{7, 3, 2, 6, 7, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 3, 11, 10, 6, 8, 10, 8, 9, 8, 6, 7, -1, -1, -1, -1},
{2, 0, 7, 2, 7, 11, 0, 9, 7, 6, 7, 10, 9, 10, 7, -1},
{1, 8, 0, 1, 7, 8, 1, 10, 7, 6, 7, 10, 2, 3, 11, -1},
{11, 2, 1, 11, 1, 7, 10, 6, 1, 6, 7, 1, -1, -1, -1, -1},
{8, 9, 6, 8, 6, 7, 9, 1, 6, 11, 6, 3, 1, 3, 6, -1},
{0, 9, 1, 11, 6, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 8, 0, 7, 0, 6, 3, 11, 0, 11, 6, 0, -1, -1, -1, -1},
{7, 11, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 6, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 8, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 1, 9, 8, 3, 1, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1},
{10, 1, 2, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 3, 0, 8, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1},
{2, 9, 0, 2, 10, 9, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1},
{6, 11, 7, 2, 10, 3, 10, 8, 3, 10, 9, 8, -1, -1, -1, -1},
{7, 2, 3, 6, 2, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 0, 8, 7, 6, 0, 6, 2, 0, -1, -1, -1, -1, -1, -1, -1},
{2, 7, 6, 2, 3, 7, 0, 1, 9, -1, -1, -1, -1, -1, -1, -1},
{1, 6, 2, 1, 8, 6, 1, 9, 8, 8, 7, 6, -1, -1, -1, -1},
{10, 7, 6, 10, 1, 7, 1, 3, 7, -1, -1, -1, -1, -1, -1, -1},
{10, 7, 6, 1, 7, 10, 1, 8, 7, 1, 0, 8, -1, -1, -1, -1},
{0, 3, 7, 0, 7, 10, 0, 10, 9, 6, 10, 7, -1, -1, -1, -1},
{7, 6, 10, 7, 10, 8, 8, 10, 9, -1, -1, -1, -1, -1, -1, -1},
{6, 8, 4, 11, 8, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 6, 11, 3, 0, 6, 0, 4, 6, -1, -1, -1, -1, -1, -1, -1},
{8, 6, 11, 8, 4, 6, 9, 0, 1, -1, -1, -1, -1, -1, -1, -1},
{9, 4, 6, 9, 6, 3, 9, 3, 1, 11, 3, 6, -1, -1, -1, -1},
{6, 8, 4, 6, 11, 8, 2, 10, 1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 3, 0, 11, 0, 6, 11, 0, 4, 6, -1, -1, -1, -1},
{4, 11, 8, 4, 6, 11, 0, 2, 9, 2, 10, 9, -1, -1, -1, -1},
{10, 9, 3, 10, 3, 2, 9, 4, 3, 11, 3, 6, 4, 6, 3, -1},
{8, 2, 3, 8, 4, 2, 4, 6, 2, -1, -1, -1, -1, -1, -1, -1},
{0, 4, 2, 4, 6, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 9, 0, 2, 3, 4, 2, 4, 6, 4, 3, 8, -1, -1, -1, -1},
{1, 9, 4, 1, 4, 2, 2, 4, 6, -1, -1, -1, -1, -1, -1, -1},
{8, 1, 3, 8, 6, 1, 8, 4, 6, 6, 10, 1, -1, -1, -1, -1},
{10, 1, 0, 10, 0, 6, 6, 0, 4, -1, -1, -1, -1, -1, -1, -1},
{4, 6, 3, 4, 3, 8, 6, 10, 3, 0, 3, 9, 10, 9, 3, -1},
{10, 9, 4, 6, 10, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 5, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 4, 9, 5, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1},
{5, 0, 1, 5, 4, 0, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1},
{11, 7, 6, 8, 3, 4, 3, 5, 4, 3, 1, 5, -1, -1, -1, -1},
{9, 5, 4, 10, 1, 2, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1},
{6, 11, 7, 1, 2, 10, 0, 8, 3, 4, 9, 5, -1, -1, -1, -1},
{7, 6, 11, 5, 4, 10, 4, 2, 10, 4, 0, 2, -1, -1, -1, -1},
{3, 4, 8, 3, 5, 4, 3, 2, 5, 10, 5, 2, 11, 7, 6, -1},
{7, 2, 3, 7, 6, 2, 5, 4, 9, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 4, 0, 8, 6, 0, 6, 2, 6, 8, 7, -1, -1, -1, -1},
{3, 6, 2, 3, 7, 6, 1, 5, 0, 5, 4, 0, -1, -1, -1, -1},
{6, 2, 8, 6, 8, 7, 2, 1, 8, 4, 8, 5, 1, 5, 8, -1},
{9, 5, 4, 10, 1, 6, 1, 7, 6, 1, 3, 7, -1, -1, -1, -1},
{1, 6, 10, 1, 7, 6, 1, 0, 7, 8, 7, 0, 9, 5, 4, -1},
{4, 0, 10, 4, 10, 5, 0, 3, 10, 6, 10, 7, 3, 7, 10, -1},
{7, 6, 10, 7, 10, 8, 5, 4, 10, 4, 8, 10, -1, -1, -1, -1},
{6, 9, 5, 6, 11, 9, 11, 8, 9, -1, -1, -1, -1, -1, -1, -1},
{3, 6, 11, 0, 6, 3, 0, 5, 6, 0, 9, 5, -1, -1, -1, -1},
{0, 11, 8, 0, 5, 11, 0, 1, 5, 5, 6, 11, -1, -1, -1, -1},
{6, 11, 3, 6, 3, 5, 5, 3, 1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 9, 5, 11, 9, 11, 8, 11, 5, 6, -1, -1, -1, -1},
{0, 11, 3, 0, 6, 11, 0, 9, 6, 5, 6, 9, 1, 2, 10, -1},
{11, 8, 5, 11, 5, 6, 8, 0, 5, 10, 5, 2, 0, 2, 5, -1},
{6, 11, 3, 6, 3, 5, 2, 10, 3, 10, 5, 3, -1, -1, -1, -1},
{5, 8, 9, 5, 2, 8, 5, 6, 2, 3, 8, 2, -1, -1, -1, -1},
{9, 5, 6, 9, 6, 0, 0, 6, 2, -1, -1, -1, -1, -1, -1, -1},
{1, 5, 8, 1, 8, 0, 5, 6, 8, 3, 8, 2, 6, 2, 8, -1},
{1, 5, 6, 2, 1, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 3, 6, 1, 6, 10, 3, 8, 6, 5, 6, 9, 8, 9, 6, -1},
{10, 1, 0, 10, 0, 6, 9, 5, 0, 5, 6, 0, -1, -1, -1, -1},
{0, 3, 8, 5, 6, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{10, 5, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 5, 10, 7, 5, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 5, 10, 11, 7, 5, 8, 3, 0, -1, -1, -1, -1, -1, -1, -1},
{5, 11, 7, 5, 10, 11, 1, 9, 0, -1, -1, -1, -1, -1, -1, -1},
{10, 7, 5, 10, 11, 7, 9, 8, 1, 8, 3, 1, -1, -1, -1, -1},
{11, 1, 2, 11, 7, 1, 7, 5, 1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 1, 2, 7, 1, 7, 5, 7, 2, 11, -1, -1, -1, -1},
{9, 7, 5, 9, 2, 7, 9, 0, 2, 2, 11, 7, -1, -1, -1, -1},
{7, 5, 2, 7, 2, 11, 5, 9, 2, 3, 2, 8, 9, 8, 2, -1},
{2, 5, 10, 2, 3, 5, 3, 7, 5, -1, -1, -1, -1, -1, -1, -1},
{8, 2, 0, 8, 5, 2, 8, 7, 5, 10, 2, 5, -1, -1, -1, -1},
{9, 0, 1, 5, 10, 3, 5, 3, 7, 3, 10, 2, -1, -1, -1, -1},
{9, 8, 2, 9, 2, 1, 8, 7, 2, 10, 2, 5, 7, 5, 2, -1},
{1, 3, 5, 3, 7, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 7, 0, 7, 1, 1, 7, 5, -1, -1, -1, -1, -1, -1, -1},
{9, 0, 3, 9, 3, 5, 5, 3, 7, -1, -1, -1, -1, -1, -1, -1},
{9, 8, 7, 5, 9, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{5, 8, 4, 5, 10, 8, 10, 11, 8, -1, -1, -1, -1, -1, -1, -1},
{5, 0, 4, 5, 11, 0, 5, 10, 11, 11, 3, 0, -1, -1, -1, -1},
{0, 1, 9, 8, 4, 10, 8, 10, 11, 10, 4, 5, -1, -1, -1, -1},
{10, 11, 4, 10, 4, 5, 11, 3, 4, 9, 4, 1, 3, 1, 4, -1},
{2, 5, 1, 2, 8, 5, 2, 11, 8, 4, 5, 8, -1, -1, -1, -1},
{0, 4, 11, 0, 11, 3, 4, 5, 11, 2, 11, 1, 5, 1, 11, -1},
{0, 2, 5, 0, 5, 9, 2, 11, 5, 4, 5, 8, 11, 8, 5, -1},
{9, 4, 5, 2, 11, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 5, 10, 3, 5, 2, 3, 4, 5, 3, 8, 4, -1, -1, -1, -1},
{5, 10, 2, 5, 2, 4, 4, 2, 0, -1, -1, -1, -1, -1, -1, -1},
{3, 10, 2, 3, 5, 10, 3, 8, 5, 4, 5, 8, 0, 1, 9, -1},
{5, 10, 2, 5, 2, 4, 1, 9, 2, 9, 4, 2, -1, -1, -1, -1},
{8, 4, 5, 8, 5, 3, 3, 5, 1, -1, -1, -1, -1, -1, -1, -1},
{0, 4, 5, 1, 0, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 4, 5, 8, 5, 3, 9, 0, 5, 0, 3, 5, -1, -1, -1, -1},
{9, 4, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 11, 7, 4, 9, 11, 9, 10, 11, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 4, 9, 7, 9, 11, 7, 9, 10, 11, -1, -1, -1, -1},
{1, 10, 11, 1, 11, 4, 1, 4, 0, 7, 4, 11, -1, -1, -1, -1},
{3, 1, 4, 3, 4, 8, 1, 10, 4, 7, 4, 11, 10, 11, 4, -1},
{4, 11, 7, 9, 11, 4, 9, 2, 11, 9, 1, 2, -1, -1, -1, -1},
{9, 7, 4, 9, 11, 7, 9, 1, 11, 2, 11, 1, 0, 8, 3, -1},
{11, 7, 4, 11, 4, 2, 2, 4, 0, -1, -1, -1, -1, -1, -1, -1},
{11, 7, 4, 11, 4, 2, 8, 3, 4, 3, 2, 4, -1, -1, -1, -1},
{2, 9, 10, 2, 7, 9, 2, 3, 7, 7, 4, 9, -1, -1, -1, -1},
{9, 10, 7, 9, 7, 4, 10, 2, 7, 8, 7, 0, 2, 0, 7, -1},
{3, 7, 10, 3, 10, 2, 7, 4, 10, 1, 10, 0, 4, 0, 10, -1},
{1, 10, 2, 8, 7, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 1, 4, 1, 7, 7, 1, 3, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 1, 4, 1, 7, 0, 8, 1, 8, 7, 1, -1, -1, -1, -1},
{4, 0, 3, 7, 4, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 8, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 10, 8, 10, 11, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 9, 3, 9, 11, 11, 9, 10, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 10, 0, 10, 8, 8, 10, 11, -1, -1, -1, -1, -1, -1, -1},
{3, 1, 10, 11, 3, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 11, 1, 11, 9, 9, 11, 8, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 9, 3, 9, 11, 1, 2, 9, 2, 11, 9, -1, -1, -1, -1},
{0, 2, 11, 8, 0, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 2, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 3, 8, 2, 8, 10, 10, 8, 9, -1, -1, -1, -1, -1, -1, -1},
{9, 10, 2, 0, 9, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 3, 8, 2, 8, 10, 0, 1, 8, 1, 10, 8, -1, -1, -1, -1},
{1, 10, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 3, 8, 9, 1, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 9, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 3, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1}};
/*
Determine the index into the edge table which
tells us which vertices are inside of the surface
*/
cubeindex = 0;
if (grid.val[0] < isolevel) cubeindex |= 1;
if (grid.val[1] < isolevel) cubeindex |= 2;
if (grid.val[2] < isolevel) cubeindex |= 4;
if (grid.val[3] < isolevel) cubeindex |= 8;
if (grid.val[4] < isolevel) cubeindex |= 16;
if (grid.val[5] < isolevel) cubeindex |= 32;
if (grid.val[6] < isolevel) cubeindex |= 64;
if (grid.val[7] < isolevel) cubeindex |= 128;
/* Cube is entirely in/out of the surface */
if (edgeTable[cubeindex] == 0)
return(0);
/* Find the vertices where the surface intersects the cube */
if (edgeTable[cubeindex] & 1)
vertlist[0] =
VertexInterp(isolevel,grid.p[0],grid.p[1],grid.val[0],grid.val[1]);
if (edgeTable[cubeindex] & 2)
vertlist[1] =
VertexInterp(isolevel,grid.p[1],grid.p[2],grid.val[1],grid.val[2]);
if (edgeTable[cubeindex] & 4)
vertlist[2] =
VertexInterp(isolevel,grid.p[2],grid.p[3],grid.val[2],grid.val[3]);
if (edgeTable[cubeindex] & 8)
vertlist[3] =
VertexInterp(isolevel,grid.p[3],grid.p[0],grid.val[3],grid.val[0]);
if (edgeTable[cubeindex] & 16)
vertlist[4] =
VertexInterp(isolevel,grid.p[4],grid.p[5],grid.val[4],grid.val[5]);
if (edgeTable[cubeindex] & 32)
vertlist[5] =
VertexInterp(isolevel,grid.p[5],grid.p[6],grid.val[5],grid.val[6]);
if (edgeTable[cubeindex] & 64)
vertlist[6] =
VertexInterp(isolevel,grid.p[6],grid.p[7],grid.val[6],grid.val[7]);
if (edgeTable[cubeindex] & 128)
vertlist[7] =
VertexInterp(isolevel,grid.p[7],grid.p[4],grid.val[7],grid.val[4]);
if (edgeTable[cubeindex] & 256)
vertlist[8] =
VertexInterp(isolevel,grid.p[0],grid.p[4],grid.val[0],grid.val[4]);
if (edgeTable[cubeindex] & 512)
vertlist[9] =
VertexInterp(isolevel,grid.p[1],grid.p[5],grid.val[1],grid.val[5]);
if (edgeTable[cubeindex] & 1024)
vertlist[10] =
VertexInterp(isolevel,grid.p[2],grid.p[6],grid.val[2],grid.val[6]);
if (edgeTable[cubeindex] & 2048)
vertlist[11] =
VertexInterp(isolevel,grid.p[3],grid.p[7],grid.val[3],grid.val[7]);
/* Create the triangle */
ntriang = 0;
for (i=0;triTable[cubeindex][i]!=-1;i+=3) {
triangles[ntriang].p[0] = vertlist[triTable[cubeindex][i ]];
triangles[ntriang].p[1] = vertlist[triTable[cubeindex][i+1]];
triangles[ntriang].p[2] = vertlist[triTable[cubeindex][i+2]];
ntriang++;
}
return(ntriang);
}
/*
Linearly interpolate the position where an isosurface cuts
an edge between two vertices, each with their own scalar value
*/
XYZ VertexInterp(isolevel,p1,p2,valp1,valp2)
double isolevel;
XYZ p1,p2;
double valp1,valp2;
{
double mu;
XYZ p;
if (ABS(isolevel-valp1) < 0.00001)
return(p1);
if (ABS(isolevel-valp2) < 0.00001)
return(p2);
if (ABS(valp1-valp2) < 0.00001)
return(p1);
mu = (isolevel - valp1) / (valp2 - valp1);
p.x = p1.x + mu * (p2.x - p1.x);
p.y = p1.y + mu * (p2.y - p1.y);
p.z = p1.z + mu * (p2.z - p1.z);
return(p);
}
It has been suggested that the interpolation should be handled as shown here, that this solves an issue of small cracks in the isosurface.
Overview by Matthew Ward
Summary
Marching Cubes is an algorithm for rendering isosurfaces in volumetric
data. The basic notion is that
we can define a voxel(cube) by the pixel values at the eight corners of the
cube. If one or more pixels
of a cube have values less than the user-specified isovalue, and one or
more have values greater than
this value, we know the voxel must contribute some component of the
isosurface. By determining
which edges of the cube are intersected by the isosurface, we can create
triangular patches which
divide the cube between regions within the isosurface and regions outside.
By connecting the patches
from all cubes on the isosurface boundary, we get a surface representation.
There are two major components of this algorithm. The first is deciding how
to define the section or
sections of surface which chop up an individual cube. If we classify each
corner as either being below
or above the isovalue, there are 256 possible configurations of corner
classifications. Two of these are
trivial; where all points are inside or outside the cube does not
contribute to the isosurface. For all
other configurations we need to determine where, along each cube edge, the
isosurface crosses, and
use these edge intersection points to create one or more triangular patches
for the isosurface.
If you account for symmetries, there are really only 14 unique
configurations in the remaining 254
possibilities. When there is only one corner less than the isovalue, this
forms a single triangle which
intersects the edges which meet at this corner, with the patch normal
facing away from the corner.
Obviously there are 8 related configurations of this sort (e.g. for
configuration 2 - you may need to
tweak the colormap to see the plane between the spheres/pixels). By
reversing the normal we get 8
configurations which have 7 corners less than the isovalue. We don't
consider these really unique,
however. For configurations with 2 corners less than the isovalue, there
are 3 unique configurations
(e.g. for configuration 12), depending on whether the corners belong to the
same edge, belong the
same face of the cube, or are diagonally positioned relative to each other.
For configurations with 3
corners less than the isovalue there are again 3 unique configurations
(e.g. for configuration 14),
depending on whether there are 0, 1, or 2 shared edges (2 shared edges
gives you an 'L' shape). There
are 7 unique configurations when you have 4 corners less than the isovalue,
depending on whether
there are 0, 2, 3 (3 variants on this one), or 4 shared edges (e.g. for
configuration 30 - again you may
need to tweak the colours to see the triangle for the isolated (far) inside
sphere/pixel).
Each of the non-trivial configurations results in between 1 and 4 triangles
being added to the
isosurface. The actual vertices themselves can be computed by interpolation
along edges, or, default their location to the middle of the edge. The interpolated
locations will obviously give you
better shading calculations and smoother surfaces.
Now that we can create surface patches for a single voxel, we can apply
this process to the entire
volume. We can process the volume in slabs, where each slab is comprised of
2 slices of pixels. We
can either treat each cube independently, or we can propagate edge
intersections between cubes which
share the edges. This sharing can also be done between adjacent slabs,
which increases storage and
complexity a bit, but saves in computation time. The sharing of edge/vertex
information also results
in a more compact model, and one that is more amenable to interpolated
shading.
It is often necessary to create normals for each vertex of the triangular faces for smooth rendering purposes. One way of doing this after the facets have been created is to average the normals of all the faces that share a triangle vertex. The following shows the smooth result on the right, the left image has the single normal for the facet applied to each it's vertices. The model below is of a particular type of neuron captured from a confocal microscope.
A common approach is at each vertex to use a weighted average of normals of the polygons sharing the vertex. The weight is the inverse of the area of the polygon, so small polygons have greater weight. The idea is that small polygons may occur in regions of high surface curvature. Example 2The original Siggraph paper computes normals at vertices by interpolating the normals at the cube vertices. These cube vertex normals are computed using Central Differences of the volumetric data.
References Lorensen, W.E. and Cline, H.E., Marching Cubes: a high resolution 3D surface reconstruction algorithm, Computer Graphics, Vol. 21, No. 4, pp 163-169 (Proc. of SIGGRAPH), 1987. Watt, A., and Watt, M., Advanced Animation and Rendering Techniques, Addison-Wesley, 1992.
Polygonising a Scalar Field Using TetrahedronsWritten by Paul BourkeJune 1997 Contribution by Dávid Tóth: DavidToth.zip
This document describes an algorithm for creating a polygonal surface representation of an isosurface through a 3D scalar field. It is closely related to the so called "marching cube" algorithm except in that case the fundamental sampling structure is a cube while here it is a tetrahedron. Method
The space is sampled at the vertices of a rectangular 3D mesh. Each mesh cell is split into 6 tetrahedrons and passed to the tetrahedron isosurface routine presented at the bottom of this document. Note that this is the approach used here, one could equally sample onto the tetrahedral mesh directly. Note that the tetrahedron edges align with those on adjacent box cells, there is a method of splitting the box into 5 tetrahedrons which doesn't have this property. The planar facet approximation to the isosurface is calculated for each tetrahedron independently. The facet vertices are determined by linearly interpolating where isosurface cuts the edges of the tetrahedron. 
There are 8 different cases, 7 are illustrated below. The hollow and filled circles at the vertices of the tetrahedron indicate that the vertices are on different sides of the isosurface. The case not illustrated is where all the vertices are either above of below the isosurface, no facets are generated in this situation. 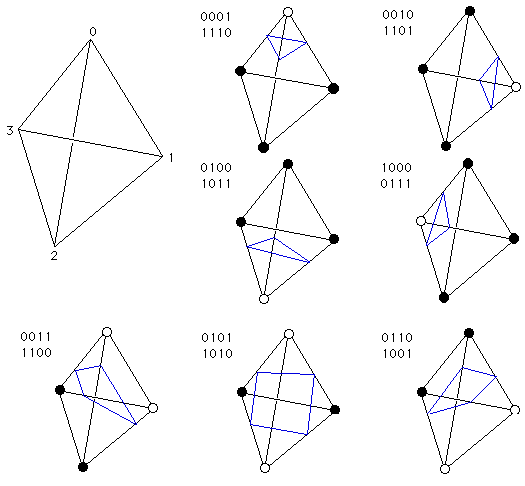 Notes
 W.Lorensen, H.Cline. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. Computer Graphics, 21 (4): 163-169, July 1987 B.A.Payne, A.W.Toga. Surface Mapping Brain Functions on 3D Models. IEEE Computer Graphics and Applications, 10 (2) 41-53, February 1990 J. Bloomenthal. Polygonisation of Implicit Surfaces. Computer-Aided Geometric Design, 5(4) 341-355, November 1988 A.Doi, A.Koide. An Efficient Method of Triangulating Equivalued Surfaces by using Tetrahedral Cells. IEICE Transactions Communication, Elec. Info. Syst, E74(1) 214-224, January 1991 A.Gueziec, R.Hummel. Exploiting Triangulated Surface Extraction using Tetrahedral Decomposition. IEEE Transactions on Visualisation and Computer Graphics, 1 (4) 328-342 December 1995
|



