Synchronous oscillation in the cerebral cortex and object coherence: simulation of basic electrophysiological findings.J.J. Wright, P.D. Bourke, C.L. ChapmanBiological Cybernetics Volume 83, Issue 4, pp 341-353, 2000. Doi: 10.1007/s004220000155
Mental Health Research Institute of Victoria,
A lumped continuum model for electrocortical activity was used to simulate several established experimental findings of synchronous oscillation which have not all been previously embodied in a single explanatory model. Moving-bar visual stimuli of different extension, stimuli moving in different directions, the impact of non-specific cortical activation upon synchronous oscillation, and the frequency content of EEG associated with synchrony were considered. The magnitude of zero lag synchrony was primarily accounted for by the properties of the eigenmodes of the travelling LFP superposition waves generated by inputs to cortex, largely independent of the oscillation properties and associated spectral content. Approximation of the differences in cross correlation observed with differently moving bar stimuli, and of the impact of cortical activation, required added assumptions on (a) spatial coherence of afferent volleys arising from parts of a single stimulus object, and (b) the presence of low amplitude diffuse field noise, with enhancement of cortical signal/noise ratio with respect to the spatially coherent inputs, at higher levels of cortical activation. Synchrony appears to be a ubiquitous property of cortex-like delay networks. Precision in the modelling of synchronous oscillation findings will require detailed description of input pathways, cortical connectivity, cortical stability, and aspects of cortical/subcortical interactions. IntroductionDiscovery of the phenomenon of synchronous oscillation in the cerebral cortex [eg Eckhorn et al 1988; Gray et al 1989; Singer 1994; Singer and Gray 1995] was partly motivated by a proposal by von der Malsburg [1983] that patterns of synchronous activity in the brain would offer a mechanism whereby the many sensory input features contributing to the perception of a unified object, might be linked to form a whole. This offered a solution to the binding problem posed by the need to register unique combinations of all possible stimulus features [Singer and Gray 1995; Livingstone 1996]. As has been pointed out by Palm and Wennekers [1997] interest in this solution to the binding problem, rather than the simpler requirements of direct modelling of experimental results has driven much of the attempts to find an explanatory mechanism for synchronous oscillation. A strong presumption that linked non-linear oscillations underlie the phenomenon [eg Abarbanel et al 1996] has motivated most attempts at modelling the phenomenon. Yet there is little evidence that phase-locking of non-linear oscillators is necessarily involved [Wennekers and Palm 1997], considering the broad spectral band over which synchrony has been found [Bressler et al 1993]. The significance of the experimental data now published on synchronous oscillation is very substantial, but remains controversial. Theoretical opinions vary from the view that synchrony may be essentially irrelevant to synaptic interactions [Amit 1998] to the possibility that synchrony is vital to the co-ordination of synaptic modifications in the brain [Phillips and Singer 1997]. Experimental conditions leave a number of variables (connectivities, signal/noise ratios etc.) unspecified. Meantime, attempts to model the process must be selective. Some experimental aspects of synchronous oscillation appear reasonably clearly defined. Firstly, it is known that synchrony is most often observed in association with oscillation in the gamma band [eg Eckhorn 1988] but not uniquely so [Bressler et al 1993]. Secondly, it appears that synchrony is strongest between cortical sites in which neurones seem to be involved in co-processing of sensory input - eg, between columns of cells with similar orientation preference [Gray and Singer 1989; Livingstone 1996]. Thirdly, it appears increased cortical activation, such as is produced by driving the mesencephalic reticular formation, enhances synchronous oscillation [Munk et al 1996]. Fourthly, properties of the stimulus object(s) play a part. One large bar moving across the visual field produces stronger synchrony than two small bars concurrently stimulating each of the relevant points in the retina, and bars moving in separate directions generally produce less synchrony than the same bars moving in the same direction across the visual field [Neuenschwander and Singer 1996; Livingstone 1996]. To attempt to provide a concise account for these experimental properties we have used a lumped continuum model of the cortex which provides an account of the general spectral content of EEG [Wright 1998]. This approach is intended to complement other simulations which approximate physiological realism using feedforward networks with inhibitory surrounds, or single and multiple orientation domains [Schillen and Konig 1994; Xing and Gerstein 1996; Fuentes et al 1996; Juergens and Eckhorn 1997]. Our object was to ascertain the minimal assumptions needed to reproduce the experimental data. The model's parameterisation is as of yet approximate, and physiological detail is incomplete, but these limitations are not relevant to the demonstrations we will report. Models closely related to that applied here have been analysed with regard to cross correlation properties under the condition that two points on the cortical surface are driven by independent white noise [Wright 1997; Robinson et al 1998; Chapman et al 1998] yielding results which have guided the experimental design used here. In this model synchrony depends wholly upon relatively long-range excitatory connections in a continuum field - dendritic lag-summations and relatively rapid axonal transmission being the essential ingredients - while short-range excitatory/inhibitory interactions appear crucial only to the occurrence of oscillation. These characteristics are very similar to those observed in neural network models with intracortical couplings only, observed by Wilson and Bower [1991]. The continuum formulation supplements the neural network approach, by enabling a different insight into the physical nature of synchrony, since the essential non-linearity of individual elements is avoided, and the stochastic and essentially linear properties of the neuronal mass is emphasised. Likewise, these intracortical two dimensional models contrast with the work of Lumer et al [1997a,b] who studied conditions for synchrony and oscillation in a neural-network model of the thalamocortical system. They observed synchrony at many levels, which they attributed largely to re-entrant activity at multiple levels in the pathway. In the present model reproduction of the physiological experiments required additional simple assumptions about the signal-to-noise ratio of cortex, and cross correlation in afferent volleys associated with individual stimulus objects, as will be described with the methods. 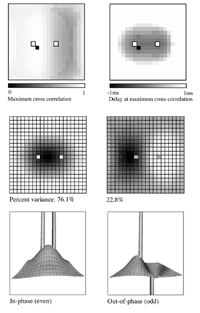
Essential properties of synchronous oscillation. Middle figures: The first and second principal eigenmodes of activity on the simulated cortical surface, obtained from the same data used to generate the top figures. Bottom figures: Schematic ``freeze frame'' images of potentials (or pulse densities) on the simulated cortical surface seen when the twin inputs are sine waves, of any single frequency. Bottom left: potentials in the field when the sine waves are in phase. Bottom right: potentials in the field when the sine waves are of reverse phase. 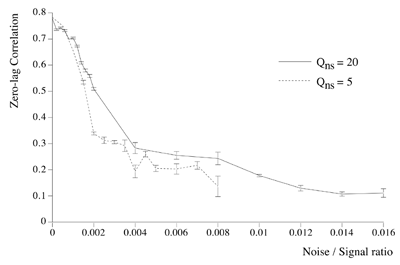 Dependency of cross-correlation on signal/noise ratio and independence from uniform cortical activation in the absence of overlying noise. Zero-lag cross correlation obtained between the reference site shown in figure 1, and another site located at the point of mirror-image symmetry, adjacent to the right hand input site. Mean and SEM of cross-correlations from 20 1s simulation runs. In addition to the twin sites of asynchronous noise input to the same driving sites as in figure 1, spatio-temporally white noise has been input to all other sites in the field. The noise-to-signal ratio refers to the ratio of rms amplitude of the random field noise, to that at the twin ``driving'' sites. Results are shown for two widely different conditions of non-specific cortical activation, as indicated by the value of parameter Qns. 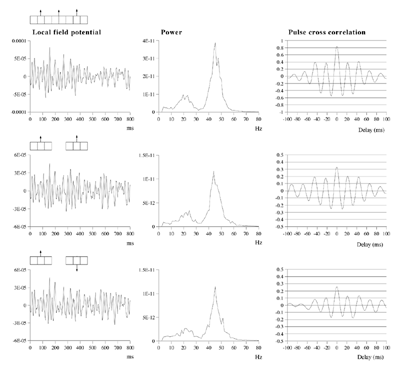
Effects of stimulus extension and coherence on synchronous oscillation. 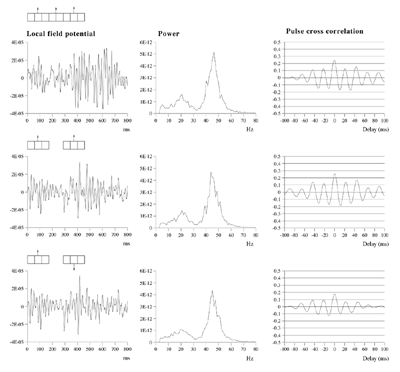 Results shown are derived as for figure 3a except that uncorrelated white noise was delivered to all parts of each bar, as well as being uncorrelated between bars. Diffuse field noise amplitude 0.000025. 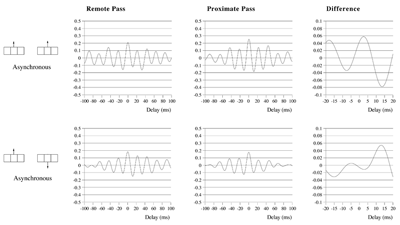 Cross-correlations for the asynchronous bar case, with diffuse field noise 0.000025, for bars moving in the same and opposite directions. Reference points at the matrix row at which the oppositely moving bars pass each other (proximate pass) or in the same columns but remote from the passing row (remote pass). See text for details. Differences are between the remote and proximate conditions. The small differences remain statistically significant. 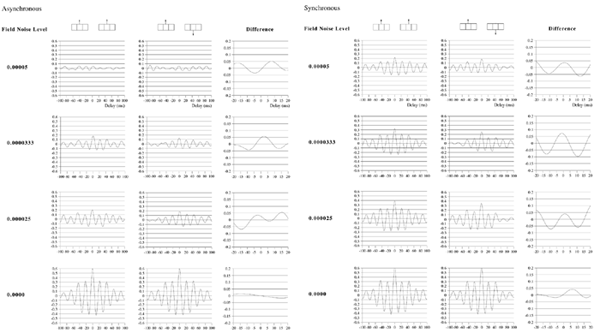 Cross-correlations from proximate-pass reference sites with differing levels of diffuse field noise, for both asynchronous and synchronous bar conditions. Differences are with respect to the directions of bar movement shown in the graphs to the left of each difference graph. The difference produced by direction of movement is zero at zero lag in the absence of diffuse field noise. 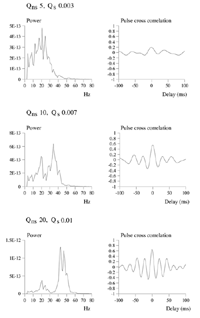 Effects of cortical activation on synchronous oscillation in the presence of uniform field noise.
Average power spectra and pulse-cross correlations calculated as for the two short bars moving in the same direction case, in figure 3a. Here uniform amplitude spatio-temporally white noise was applied throughout the field, and both the level of cortical activation (Qns) and the amplitude of the signals associated with the moving bars (Qs) were raised concurrently.
ReferencesAmit DJ (1998),Simulation in neurobiology: theory or experiment? TINS 21: 231-237.
Abarbanel H, Rabinovich M,
Selverston A, Bazhenov M, Huerta R,
Sushchik M (1996).
Alexander DM, Bourke PD, Sheridan P,
Konstandatos O, Wright JJ (1999)
Bressler SL, Coppola R, Nakamura R (1993)
Chapman CL, Bourke PD, Wright JJ (1998)
Eckhorn R, Bauer R, Jordon W, Brosch M,
Kruse W, Munk M, Reitboeck HJ (1988)
Fuentes U, Ritz R, Gerstner W, Van Hemmen JL (1996)
Ghose GM, Freeman RD (1997)
Gray CM, Singer W (1989)
Gray CM, Konig P, Engel AK, Singer W (1989)
Juergens E, Eckhorn R (1997)
Kandel ER, Schwartz JH (1985)
Kreiter AK, Singer W (1996)
Liley DTJ, Wright JJ (1994)
Livingstone MS (1996)
Lumer ED, Edelman GM, Tononi G (1997a)
Lumer ED, Edelman GM, Tononi G (1997b)
Malach R, Amir Y, Harel M, Grinvald A (1993)
von der Malsburg C (1983)
Marsaglia G, Zaman A (1987)
Miltner WH, Braun C, Arnold M, Witte H, Taube E (1999)
Munk MHJ, Roelfsema PR, Konig P, Engel AK, Singer W. (1996)
Neuenschwander S, Singer W (1996)
Nunez PL (1995)
Palm G, Wennekers T (1997)
Phillips WA, Singer W (1997)
Preisendorfer, R. (1988).
Robinson PA, Rennie CJ, Wright JJ (1997)
Robinson PA, Wright JJ, Rennie CJ (1998)
Rodriguez E, George N, Lachaux JP,
Martinerie J, Renault B, Varela FJ (1999)
Ruiz S, Crespo P, Romo R (1995)
Schillen TB, Konig P (1994)
Segev I. (1995)
Singer W. (1994)
Singer W., Gray CM. (1995)
Steriade M, Amzica F, Contreras D (1996)
Stryker MP (1989)
Thomson AM (1997)
Thomson AM, West DC, Hahn J, Deuchars J (1996)
Wang, D. (1996).
Wennekers T, Palm G. (1997).
Wilson MA, Bowers JM (1991)
Wright JJ (1997)
Wright JJ (1998)
Xing J, Gerstein GL (1996)
Yoshioka T, Blasdel GG, Levitt JB, Lund JS (1996) |