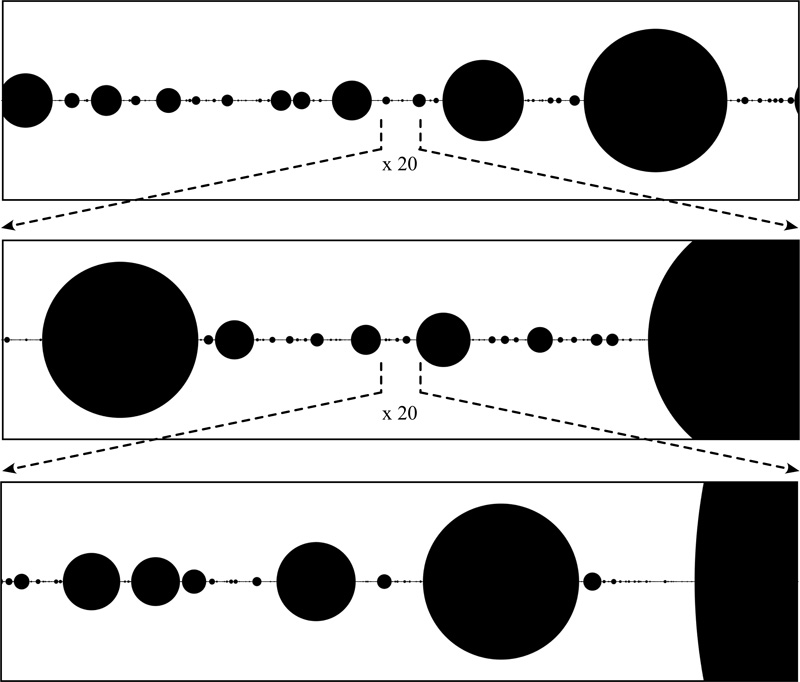
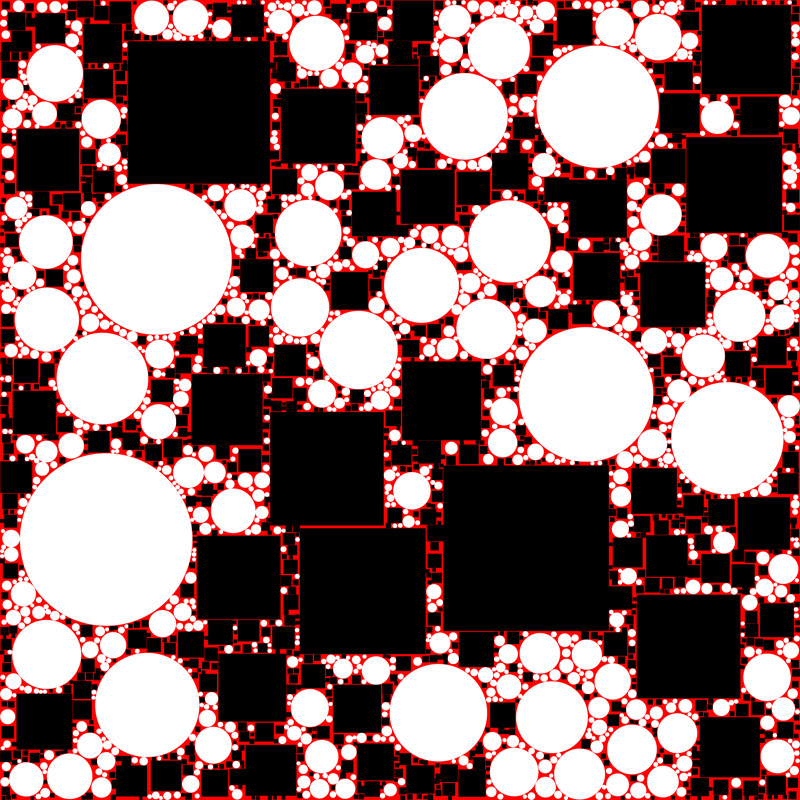
An Algorithm for Random Fractal Filling of SpaceJohn Shier1, Paul Bourke2Computer Graphics Forum. The Eurographics Association and John Wiley & Sons Ltd. doi: 10.1111/cgf.12163
1Normandale Community College, Bloomington, Minnesota 55431, USA.
Computational experiments with a simple algorithm show that it is possible to fill any spatial region with a random fractalization of any shape, with a continuous range of pre-specified fractal dimensions D. The algorithm is presented here in 1, 2, or 3 physical dimensions. The size power-law exponent c or the fractal dimension D can be specified ab initio over a substantial range. The method creates an infinite set of shapes whose areas (lengths, volumes) obey a power law and sum to the area (length, volume) to be filled. The algorithm begins by randomly placing the largest shape and continues using random search to place each smaller shape where it does not overlap any previously placed shape. The resulting gasket is a single connected object. Categories and Subject Descriptors (according to ACM CCS):G.3 [Mathematics of Computing]: Probability and Statistics--Stochastic processes, I.3.5 [Computer Graphics]: Computational Geometry and Object Modeling--Geometric algorithms, languages, and systems, I.3.m [Computer Graphics]: Miscellaneous Paper (Pre-Review): PDF fileSelected figures from the paper

|