3D volumetric fractal trajectoriesWritten by Paul BourkeJuly 2018 Inspired by Shawn Halayka: Visualizing the Escape Paths of Quaternion Fractals
The following are the trajectories of the points that diverge to infinity for a number of 3D volumetric fractals. The way these Mandelbrot style fractals are normally rendered is to consider points within some region and evaluate the series associated with the fractal. The behaviour of the series is then encoded in colour for that point. Typically these points converge, diverge or oscillate. Here only the points that diverge to infinity are considered, the path they take is drawn as a Bezier curve. In 2D this is related to the buddhabrot which illustrates the path the series takes as points diverge to infinity for the Mandelbrot set. 





One is not constrained to trace the escape paths for 3D fractals, the following are from the traditional Mandelbrot, essentially a 3D version of the Buddhabrot but less "interesting". 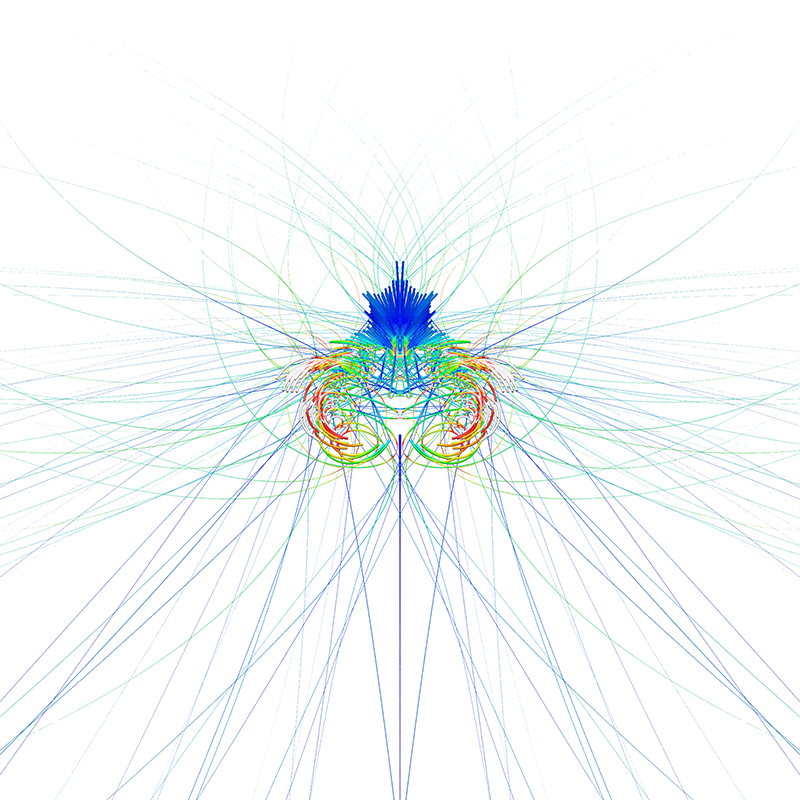

|