Wada basins

Rendering chaotic scattering

Introduction

The following is a computer rendering that replicates the results of experiments in chaotic scattering. Application of this occur in such diverse disciplines as fluid dynamics, cosmology, celestial mechanics, thermodynamics, and atomic scattering. The basic setup is four identical, highly reflective balls sitting is a pyramid formation so that each ball touches every other ball. One looks into the gaps between three balls and either shines light into all or one of the other gaps or places coloured paper over the gaps and shines light into the same gap one is looking into (or variations of the above). The resulting multitude of reflections, fractal, has what is known as the Wada property after the Japanese mathematician who studied these spatial divisions in 1917. The Wada property refers to cases when there are three basins of attractions so convoluted that every point on a basin boundary is also on the boundary of all other basins.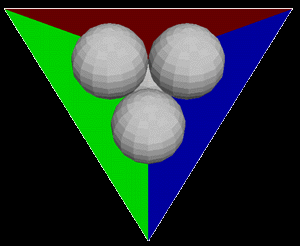

You can do the real experiments yourself by getting 4 Christmas tree balls or other shiny balls, placing coloured paper over some of the gaps and/or shining light into the gaps. Unfortunately the physical experiment can't be exactly replicated with rendering software because raytracers don't trace light from the light sources back to the camera, rather they trace "fake" rays from the camera back into the scene and finally to the lights. The following image is a rendering from a position where the balls and coloured planes can all be seen, for the coordinates of the geometry see balls5.dat.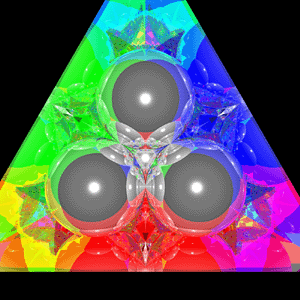

The most important setting for a raytracer in order to replicate the results here is to be able to set the number of reflections that will be considered for each ray. Typically raytracers only trace back about 6 intersections before they evaluate the light contribution, for this exercise the more reflections the better the result.

Tachyon

The images here were rendered using the Tachyon rendering package written by John Stone. The same results could be achieved with almost any raytracer, in particular PovRay, Radiance, etc. As mentioned before it is important to be able to set the ray trace depth, it is also important to be able to precisely set the position and radius of the balls to avoid any narrow slits or intersections. The table below gives the centre and radius of the 4 balls in the configuration used here.

      x      y      z         r
    -0.5   -0.5    0.5   sqrt(2) / 2 
     0.5    0.5    0.5   sqrt(2) / 2 
    -0.5    0.5   -0.5   sqrt(2) / 2 
     0.5   -0.5   -0.5   sqrt(2) / 2

In this example (balls2.dat) a light is positioned behind the camera illuminating the gap between the three front balls.

Models in Tachyon format are given below for the three basic model configurations illustrated by the images on this page.
balls1.dat
balls2.dat
balls3.dat
balls5.dat

PovRay

For those who like PovRay, here is a model to use as a starting point for exploration.
wada.ini
wada.pov

Third place (Artistry section) in the PovRay short code contest.

global_settings {max_trace_level 1000}
#declare a=sqrt(2);
#declare r=texture{pigment{color<1,1,1>}finish{ambient 0
diffuse 1 reflection 1}}
camera{location x-y+z look_at<0,0,0>}
light_source{<-3,-3,-3>color<0,1,0>}
light_source{<-3, 3, 3>color<0,0,1>}
light_source{< 3, 3,-3>color<1,0,0>}
sphere{z-x-y,a texture{r}}
sphere{x+y+z,a texture{r}}
sphere{y-x-z,a texture{r}}
sphere{x-y-z,a texture{r}}

Radiance

The following files might be useful as a way of starting your exploration using the Radiance tracer.

Vivid

A Vivid model (wada.v) contributed by Rasta Robert, example renderings are given below.

Polyray

A Polyray model (wada.pi) contributed by Rasta Robert.

Bryce

Contribution by Luc Benard, 3 silver spheres and one gold with a pink cube in the inner space. Bryce model: FB1.br5.

Further examples

In this and subsequent examples (wada3.dat) the coloured paper covering the gaps has been replaced by coloured light sources. There is a coloured light at three of the gaps and the camera is located at the other gap.

You can generate this rendering at high resolutions and the colour of any particular spot on the spheres will be arbitrarily close to another colour.

The left image below is a view from the origin looking out one of the gaps with a single green light source shining into the same gap (the light source itself can't be seen). The image on the right is looking in the opposite direction.

"Sitting" at the origin looking at one of the touching points of two spheres (on the left).

References

Complex topology in chaotic scattering: a laboratory observation
D. Sweet, E. Ott, J.A. Yorke.
Nature 399, 315 (1999)

Basins of Wada
Kennedy, J. & Yorke, J.A.
Physica D 51, 213-225, 1991

Chaotic scattering in several dimensions
Q. Chan, M. Ding, E Ott.
Phys Letters. A 115, 93-100 (1990)

Fractal basin boundaries
McDonald, S.W., Grebogi, C., Ott, E. & Yorke, J.A.
Physica D 17, 125-153, 1985

Fractal basin structure
Takesue, S. & Kaneko, K.
Progr. Theor. Phys. 71, 35-49, 1984

Fractal and Wada basin boundaries in quasiperiodically driven systems
U. Feudel, A. Witt, Y.-C. Lai, and C. Grebogi
Physical Review E 58, 3060-3066 (1998).

Basins of attraction
H.E. Nusse, J.A. Yorke
Science 271, 1376-1380 (1996)